
青少年特发性脊柱侧弯的病因不清楚,导致在诊断治疗上出现许多误区,病机不清直接导致治疗无效。故有必要对其进行深入的剖析,下面我们从生物力学、材料力学、结构力学的角度来分析脊柱侧弯的特征。
胡克定律
胡克定律由R.胡克于1678年提出,表达式为F=-kx,弹簧在发生弹性形变时,弹簧的弹力F和弹簧的伸长量(或压缩量)x成正比,k是物质的弹性系数,它只由材料的性质所决定,与其他因素无关。负号表示弹簧所产生的弹力与其伸长(或压缩)的方向相反。
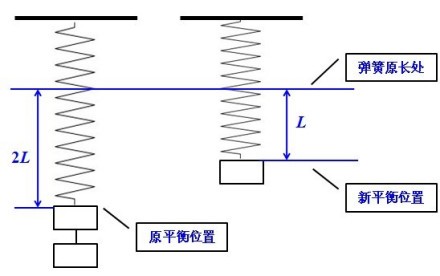
脊柱的简化物理模型
• 脊柱侧向的S形生理弧度、椎间盘,使脊柱符合胡克定律的简化物理模型。
• 脊柱受外力压缩或拉伸后,恢复形变的弹力与压缩或拉伸量呈正比。当然还要考虑脊柱本身的强度及性质。
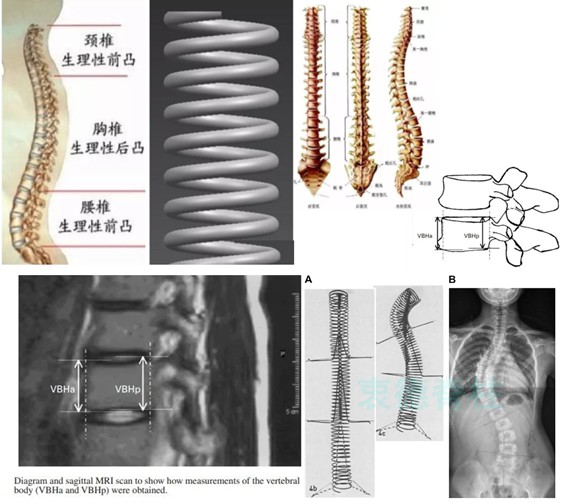
失稳
• 在服从胡克定律的前提下
• 细长直杆,当轴向压力(P)比较小时,杆受到横向的干扰力作用会发生微小的弯曲,但当干扰力消失后,仍会回到原有平衡位置,这时杆的直线平衡状态是稳定的;当压力(P)增大到某一数值(Pcr)时,如杆受到横向的干扰力使其偏离直线位置后,不能恢复到原有的直线平衡状态,这种现象称为失稳,或称屈曲。
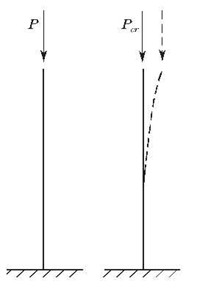
欧拉临界荷载
• 早在1744年,欧拉就发现了这种现象并加以研究,并在文章中首次对这种现象进行了定量的数学描述,在文章中对压杆进行了理想情况下的数学推演,并计算出了失稳临界荷载。后来人们为了纪念欧拉对此作出的贡献,将这个荷载值称为欧拉临界荷载(Pcr)或欧拉荷载。相应的应力称为临界应力,用σcr表示。
载荷与失稳
• 两端相对固定的细长杆,两端施加压力P,P超过欧拉载荷临界值,杆发生侧弯,压力、材料弹性模量和横截面不变,杆越长,侧弯越明显。
• 这里还可引入柔度(长细比)λ=l/i;柔度与杆长成正比,与截面半径呈反比。
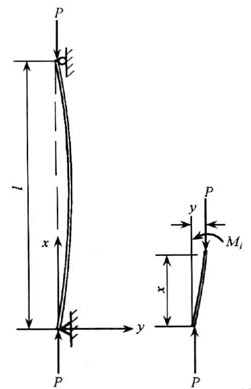
这可以很好解释为什么脊柱侧弯多发生在廋高个,罕见于矮胖墩。

载荷变化与失稳
• 对于小于临界载荷的载荷,柱子将保持笔直。
• 临界载荷是不会引起横向变形(屈曲)的载荷。
• 临界载荷使柱处于不稳定的平衡状态。
• 对于大于临界载荷的载荷,柱将横向偏斜。
• 超过临界载荷的载荷会导致柱因屈曲而失稳。
• 当载荷增加到超过临界载荷时,横向变形会增加,直到它可能以其他模式失效,例如材料屈服。
• 推理:当弹性模量不变,载荷增大可能是脊柱侧弯的病因。
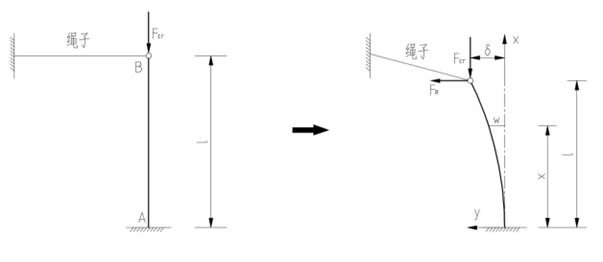
侧向不对称外力
• 如图所示,空心细长杆弹性模量、长度、外径、内径均已知,细长杆一端与地面固定,另一端与不可伸长的绳相连,仅考虑平面内稳定性,由于绳不可伸长,故杆受压时只能往左侧弯曲。
• 但,当干扰力消失后,可能会回到原有平衡位置。
推理:姿势不正与脊柱侧弯有关联,但不是决定因素。我们从骨折固定后关节僵硬以及早期康复尽早活动关节的机制也能得出相同推理。
完全稳定与部分稳定
• 完全稳定的柱是指柱在外力作用下,不发生任何形状的变化和扭曲,保持初始长度和几何形状。在完全稳定的情况下,柱仅受压应力作用,应力沿柱轴线均匀分布。此时柱的稳定性完全由初始几何形状和材料强度决定。
• 部分稳定的柱是指柱在外力作用下,产生轻微的形状变化和扭曲,但不引起整体破坏。部分稳定柱的稳定性除与初始几何形状和材料强度有关外,还与柱的几何缺陷、加载条件、荷载形式等因素紧密相关。
脊柱侧弯尤其是青少年,在全脊柱片上看,除整体上脊柱发生了侧弯形变,但椎体并无明显形状变化,这对康复矫形训练无疑是好消息。